Piramida

Bir çoxüzlü bucaq götürək və onun bütün tillərini kəsən müstəvi keçirək. 

Çoxüzlü bucaqın S təpəsinin aid olduğu yarımfəzada SABDEF çoxüzlüsü alınır. 

Bu çoxüzlünün bir üzü ABCDEF çoxbucaqlısı qalan üzləri isə bir təpəsi S olan ortaq təpəsi üçbucaqlıdır. 

ASB, BSC,........, FSA, belə çoxüzlülər piramida adlanır.

Ortaq təpəli üçbucaqlara piramidanın yan üzləri, onların birləşməsinə piramidanın yan səthi, 

çoxbucaqlıya piramidanın oturacağı, 

bütün yan üzlərin ortaq tərəfinə piramidanın yan tilləri, təpədən oturacaq müstəvisinə çəkilmiş perpendikulyara piramidanın hündürlüyü deyilir.

Bir üzü hər hansı çoxbucaqlı, qalan üzləri ortaq təpəli üçbucaqlar olan çoxüzlüyə piramida deyilir.

Piramida Oturacağındakı çoxbucaqlının adı ilə adlandırılır. Üçbucaqlı, dördbucaqlı, beşbucaqlı,....... n bucaqlı piramida
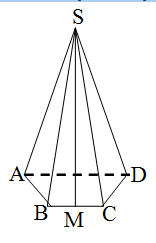
Yan üzdə təpədən oturacağın tərəfinə çəkilmiş hündürlüyə apofem deyilir.(SM)

Oturacağı düzgün çoxbucaqlı və hündürlüyünün oturacağı bu çoxbucaqlının mərkəzi olan piramidaya düzgün piramida deyilir. Düzgün piramidanın hündürlüyünün saxlayan düz xəttə onun oxu deyilir.

Teorem 
Düzgün piramidanın yan səthinin sahəsi oturacağın perimetri ilə apofemi hasilinin yarısına bərabərdır.

Piramidamım tam səthinin sahəsi yan səthinin sahısi ilə oturacağının sahəsinin cəminə bərabərdir.

S tam = S yan + S ot

KƏSIK PİRAMİDA

Bir piramida götürək və onu oturacağına paralel müstəvi ilə kəsək. Onda S nöqtəsindən çıxan süaları kəsən iki paralel müstəvi alırıq (kəsik və oturacaq.)

Teorem . Piramidada paralel kəsik
Piramidanın oturacağına paralel və onun kəsən müstəvi:
1) piramidanın yan tillərini və hündürlüyünü mütanasib parçalara böür
2) kəsikdə alınan çoxbucaqlı oturacağa oxşardır və oxşarlıq əmsalı onları təpədən olan məsafələri nisbətinəbərabərdir.
3) kəsiyin və oturacağın sahələri nisbəti oxşarlıq əmsalının kvadratına, yaxud onların təpədən olan məsafələrinin kvadratları nisbətinə bərabərdir.

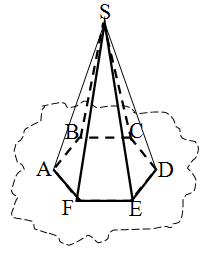
Piramidanın oturacağına paralel və onu kəsən müstəvi ilə oturacağı arasında qalan çoxüzlüyə kəsik piramida deyilir.

Kəsik piramidanın paralel üzlərinə onun oturacaqları, yan üzlərinə isə yan səthi deyilir. 

Kəsik piramidanın yan səthi trapesiyalardan ibarətdir. Oturacaq müstəviləri arasındakı məsafəyə kəsik piramidanın hündürlüyü deyilir. 

Düzgün piramidanı oturacağına paralel müstəvi ilə kəsdikdə alınan kəsik piramidaya düzgün kəsik piramida deyirlir.
Düzgün kəsik piramidanın yan üzləri bir-birinə bərabər olan bərabəryanlə trapesiyalardır.

Teorem . düzgün kəsik piramidanın yan səthi
Düzgün kəsik piramidanın yan səthinin sahəsi onun oturacaqlarının perimetrləri cəminin yarısı ilə apofemi hasilinə bərabərdir

Kəsik piramidanın bir üz üzərində olmayan iki yan tilindən keçən müstəvi ilə kəsiyinə dioqanal kəsiyi deyilir.