29.10.2015

10/29/2015 06:53:00 ÖS

Nəzəri Biliklər

Cəbri düz və tərs mütənasiblik

Mütənasib

Mütənasib - iki kəmiyyətdən birinin artması (azalması) ilə o biri kəmiyyətində eyni dərəcədə artması (azalması)

Mütənasib ölçülərin dəyişməz münasibəti mütənasiblik əmsalı adlanır.

'∝' riyazi simvolu iki ölçünün mütənasibliyinin göstərilməsi üçün istifadə olunur. Nümunə, A ∝ B.

Yunikod kodlaşdırılmasında simvolun qısayol keçidi: U+221D.

Düz mütənasibliyin qrafiki koordinat başlanğıcından keçən düz xətdir.

Düz mütənasiblik

Düz mütənasiblik — arqumentin (x) neçə dəfə artması ilə funksiyanında (y) bir o qədər artmasının funksional asılığıdır.

Riyaziyyatda düz mütənasiblik ifadəsi aşağıdakı düstur şəklində yazılır:

f (x) = kx, k = const

Tərs mütənasiblik

y=\frac{ k}{ x}, x\neq 0, k\neq 0

Tərs mütənasiblik — arqumentin neçə dəfə artması ilə funksiyanın bir o qədər azalmasının funksional asılılığıdır.

Funksiyanın xüsusiyyətləri:

Bir neçə funksiyanın qrafikləri: ;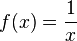

f(x) = \frac {1} {x}

;

f(x) = -\frac {1} {x}

;

f(x) = -\frac {12} {x}

Təyin oblastı

D (y) = (-\infty; 0) \cup (0; +\infty)

Qiymətlər oblastı $E (y) = (-\infty; 0) \cup (0; +\infty)$
Funksiya təkdir, çünki $f(-x) = \frac {k} {-x} = - \frac {k} {x} = -f(x)$
Funksiya k>0 olduqda $(-\infty; 0)$ aralığında azalır və $(0; +\infty)$ artır (k<0 olduqda əks proses).

Mənbə: Riyaziyyat

0 Şərh:

Xahiş edirəm təkcə yazı ilə bağlı öz rəylərinizi qeyd edəsiniz...
Şəxsi suallar,öyrənmək və soruşmaq istədikləriniz varsa,əlaqə formu və ya informasiya formu
Rəy, tövsiyyə və iradlarınız üçün isə Qonaq Dəftəri dən istifadə edin!

Kaydol: Kayıt Yorumları (Atom)